ALIŞTIRMALAR: 32'NİN ÇARPAN AĞACI ALIŞTIRMA 1'İN ÇÖZÜMLERİ
Çarpan ağacı yöntemini kullanarak aşağıdaki sayıları çarpanlarına ayırın.
a'nın çözümü
32'yi asal çarpanlarına ayıralım.

Çarpımları
a)
Bu alternatiflerden

Dalların ucuna yazdığımız
Önce
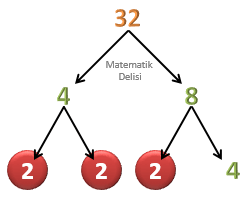

Daha önce yaptığımız gibi
Daire içerisine aldığımız sayıları çarparak
