ÇIKMIŞ SORULAR: ÖZDEŞLİKLERLE İLGİLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ-1
| LGS'DE ÇIKAN SORU SAYISI | |||||||
|---|---|---|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | 2023-2024 | |
| Soru Sayısı | 1 | 1 | 2 | 1 | 1 | 0 | 0 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 1 |
| 2018-2019 | 1 |
| 2019-2020 | 2 |
| 2020-2021 | 1 |
| 2021-2022 | 1 |
| 2022-2023 | 0 |
| 2023-2024 | 0 |
Aşağıda, LGS'de özdeşliklerle ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 5 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için sonraki sayfaya geçebilirsiniz.
2017-2018 LGS
Aşağıdakilerden hangisi
3x2 – 6xy + 3y2
cebirsel ifadesinin çarpanlarından biridir?
Çözüm:
Katsayıların tümü 3'ün tam katı olduğu için bu ifadeyi 3 parantezine alalım.
3x2 – 6xy + 3y2 = 3(x2 – 2xy + y2)
Parantez içerisindeki ifade (x – y)2'ye eşittir. Aynı zamanda bu ifade (y – x)2'ye de eşittir. Bu nedenle çarpanlarından biri y – x'tir.
CEVAP: B
2018-2019 LGS
Dik üçgenlerde 90° lik açının karşısındaki kenara hipotenüs denir.
Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı, hipotenüsün uzunluğunun karesine eşittir.

a2 + c2 = b2
Geometri tahtası, bir zeminin üzerine eşit aralıklarla yerleştirilmiş çivilerden oluşur.
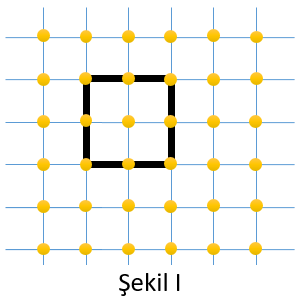

Şekil I’deki geometri tahtasında oluşturulan karenin alanı ... ... birimkaredir.
Bu geometri tahtasında Şekil II’deki gibi oluşturulan üçgenin çevre uzunluğu x cinsinden kaç birimdir?
Çözüm:
Şekil I'deki geometri tahtasında oluşturulan karenin alanı ... ... ... birimkaredir. Buna göre, karenin kenar uzunluğu ... ... birimdir.
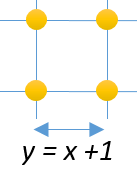
İki komşu çivi arasındaki uzaklığa ... dersek, karenin kenar uzunluğu ... olur. Bu uzunluk ...'ye eşit olduğu için ... ... birimdir.
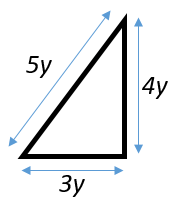
Şekil II'deki üçgenin dik kenar uzunlukları ... ve ... birimdir. Pisagor Teoremi'ni kullanarak, hipotenüs uzunluğunun ... olduğunu görebiliriz.
... ... ... ...
Üçgenin çevresi kenar uzunluklarının toplamına eşittir.
Üçgenin Çevresi = ... ...
... ifadesinde ... yerine ... yazdığımızda, sonucun ... birim olduğunu görebiliriz.
... ... ...
CEVAP: A
2019-2020 LGS
Aşağıda çevresinin uzunluğu (2x + 2) m olan dikdörtgenlerden yeterli sayıda verilmiştir.

Bu dikdörtgenler [AB] boyunca sırasıyla önce uzun kenarı sonra kısa kenarı üzerine aralarında boşluk kalmayacak şekilde aşağıdaki gibi yerleştirilmiştir. Uzun kenarı üzerine yerleştirilen ilk dikdörtgenin bir köşesi A noktası ile kısa kenarı üzerine yerleştirilen son dikdörtgenin bir köşesi B noktası ile çakışıktır.

Bu dikdörtgenler (x + 1) kez kısa kenarı üzerine yerleştirildiğine göre [AB]’nın uzunluğunu metre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
Çözüm:
... kez kısa kenarı üzerine yerleştirilen bu dikdörtgen, ... kez de uzun kenarı üzerine yerleştirilmiştir. Bu nedenle, A ve B noktaları arasındaki mesafe, ... kısa kenarla ... uzun kenarın toplam uzunluğuna eşittir. Bir dikdörtgenin 1 kısa kenarı ile 1 uzun kenarının toplamı, çevresinin yarısıdır. Dolayısıyla, A ile B arasındaki uzaklık ... tane çevreye eşittir.
... ... ... ...
CEVAP: D
Kare şeklindeki boş bir panoya kare şeklindeki üç eş mavi karton, köşegenleri panonun köşegeni ile çakışacak şekilde aşağıdaki gibi yerleştirilmiştir.

Panoda boş bırakılan bölgelerin alanları toplamı 6x2 + 36x + 54 santimetrekaredir. Kartonların üst üste gelen bölgelerinin her biri, alanları 1 cm2 olan karesel bölgelerdir.
Buna göre panonun çevresinin uzunluğunu santimetre cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
Çözüm:
Panoda boş bırakılan bölgelerin toplam alanı santimetrekare cinsinden
6x2 + 36x + 54 = 6(x2 + 6x + 9) = 6(x + 3)2'dir.

Boş kalan bölgeler yukarıdaki gibi 6 eş kareye ayrılabilir. Bu karelerden her birinin alanı 6(x + 3)2 ÷ 6 = (x + 3)2 cm2 ve kenar uzunluğu x + 3 cm'dir. Mavi karenin kenar uzunluğu, bu uzunluktan 1 cm fazladır. Buna göre panonun kenar uzunluğu x + 3 + x + 3 + x + 4 = 3x + 10 cm'dir.
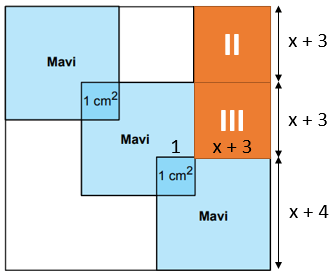
Panonun çevresi, kenar uzunluğunun 4 katıdır.
4(3x + 10) = 12x + 40 cm
CEVAP: A
2020-2021 LGS
Kare şeklindeki bir kâğıdın bir yüzü aşağıdaki gibi sekiz eş beyaz bölgeye ve dört eş mavi bölgeye ayrılmıştır.

Beyaz bölgelerden her biri, alanı (4x2 + 8x + 4) cm2 olan karesel bölgelerdir.
Buna göre mavi bölgelerden birinin alanını santimetrekare cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
Çözüm:
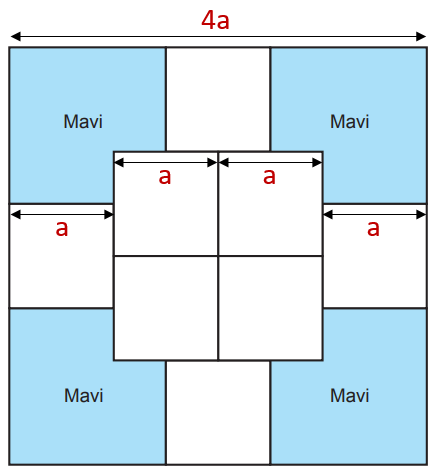
Santimetre cinsinden beyaz kenar uzunluğuna a dersek kare şeklindeki kâğıdın kenar uzunluğu 4a cm ve alanı (4a)2 = 16a2 cm2 olur. Kâğıttaki beyaz karelerden her birinin alanı a2 cm2'ye eşit olduğundan bu karelerin kapladığı toplam alan 8a2 cm2'dir. Geriye kalan 16a2 – 8a2 = 8a2 cm2'lik kısım ise mavi bölgeye aittir.
Kâğıtta toplam 4 eş mavi bölge olduğundan bu bölgelerden her birinin alanı 8a2 ÷ 4 = 2a2 cm2'dir.Kısacası, bir mavi bölgenin alanı, beyaz karenin alanının 2 katıdır. Beyaz bölgelerden birinin alanı
a2 = 4x2 + 8x + 4 = 4(x2 + 2x + 1) = 4(x + 1)2
şeklinde ifade edilebildiği için mavi bölgelerden birinin alanını veren cebirsel ifade
2 . 4(x + 1)2 = 8(x + 1)2'dir.
CEVAP: B
