Üslü Sayılarla
İşlemler
Ondalık
Gösterim

SINIF 8KONULARKONU 16BÖLÜM 1

8.SINIF

MATEMATİK DELİSİ

ÜSLÜ SAYILAR

KONU 16: ÇÖZÜMLEME

BÖLÜM 1: TAM SAYILARIN ÇÖZÜMLEMESİ (TEKRAR)

BÖLÜM 1: TAM SAYILARIN ÇÖZÜMLEMESİ (TEKRAR)

Bu bölümünde, tam sayıların 10'un kuvvetleri ile çözümlenmesi konusunu tekrarlıyoruz. Sonraki bölümde ise, ondalıklı gösterimin çözümlemesinin nasıl yapıldığını öğreniyoruz.

 

TAM SAYILARIN ÇÖZÜMLEMESİ (TEKRAR)

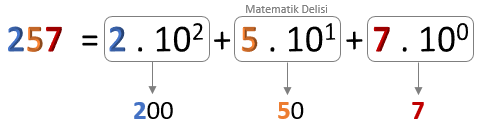
Çözümleme örneği

Bir sayının çözümlemesini yaparken, bu sayıyı basamak değerlerinin toplamına eşitleriz. Basamak değerlerinin her birini de, ilgili basamaktaki rakamla 10'un kuvvetlerinin çarpımı şeklinde yazarız.

27 236 sayısını çözümleyelim.

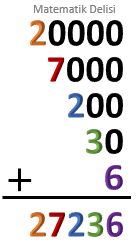
Çözümleme örnek 1

27 236'yı basamak değerlerinin toplamı şeklinde aşağıdaki gibi yazabiliriz.

27 236 = 20 000 + 7000 + 200 + 30 + 6

Yukarıdaki toplamı çözümlemeye dönüştürebilmek için eşitliğin sağındaki her bir basamak değerini, bu basamaktaki rakamla 10'un bir kuvvetinin çarpımı şeklinde yazmamız gerekir.

  • 20 000 = 2 . 10 000 = 2 . 104
  • 7000 = 7 . 1000 = 7 . 103
  • 200 = 2 . 100 = 2 . 102
  • 30 = 3 . 10 = 3 . 101
  • 6 = 6 . 1 = 6 . 100

Basamak değerleri yerine yukarıda bulduğumuz üslü gösterimleri yazarak, 27 236'nın çözümlemesini elde edebiliriz.

27 236 = 2 . 104 + 7 . 103 + 2 . 102 + 3 . 101 + 6 . 100

  • 18 792 = 1 . 104 + 8 . 103 + 7 . 102 + 9 . 101 + 2 . 100
  • 4 746 352 = 4 . 106 + 7 . 105 + 4 . 104 + 6 . 103 + 3 . 102 + 5 . 101 + 2 . 100
  • 7 = 7 . 100
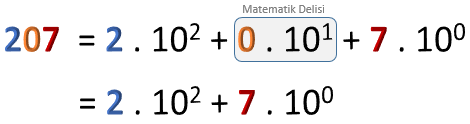
Çözümleme ve 0 rakamı

0 olan basamakların basamak değeri de 0'dır. Bu basamaklar çözümlemede göz ardı edilebilir.

2003'ü çözümleyelim.

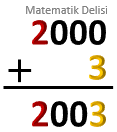
Sıfırlı sayının çözümlemesi

2003'ün basamak değerlerinin toplamı aşağıdaki gibidir.

2003 = 2000 + 3

Basamak değerlerini, basamaktaki rakamlarla 10'un kuvvetlerinin çarpımı şeklinde yazdığımızda, aşağıdaki çözümlemeyi elde ederiz.

2003 = 2 . 103 + 3 . 100

Sıfır olan basamakları da çözümlemeye katarsak, aşağıdaki eşitliği elde ederiz.

2003 = 2 . 103 + 0 . 102 + 0 . 101 + 3 . 100

Yukarıda bulduğumuz çözümlemelerin ikisi de doğrudur.

  • 30 802 = 3 . 104 + 8 . 102 + 2 . 100
  • 25 000 037 = 2 . 107 + 5 . 106 + 3 . 101 + 7 . 100
  • 1000 = 1 . 103

Aşağıdaki tam sayıları 10’un kuvvetleri ile çözümleyin.

a) 45 = ..., b) 7777 = ..., c) 100 001 = ..., d) 7 458 085 = ..., e) 12 002 100 = ..., f) 88 800 = ...

CEVAPLAR

 

Aşağıdaki hesaplama aracını kullanarak istediğiniz tam sayıların çözümlemesini yaptırabilirsiniz.

 
 

ALIŞTIRMALARIN CEVAPLARI

Alıştırmalar-1

a) 45 = 4 . 101 + 5 . 100

b) 7777 = 7 . 103 + 7 . 102 + 7 . 101 + 7 . 100

c) 100 001 = 1 . 105 + 1 . 100

d) 7 458 085 = 7 . 106 + 4 . 105 + 5 . 104 + 8 . 103 + 8 . 101 + 5 . 100

e) 12 002 100 = 1 . 107 + 2 . 106 + 2 . 103 + 1 . 102

f) 88 800 = 8 . 104 + 8 . 103 + 8 . 102

Sorulara Dön

HATIRLATMA:

1 = 100

10 = 101

100 = 102

1000 = 103

10 000 = 104

100 000 = 105

1 000 000 = 106

10 000 000 = 107

100 000 000 = 108

.....

 

→KONU ANASAYFASINA DÖN←

Çözümleme Konusuna Git

ÖNCEKİ BÖLÜM

KONU 15: ÜSLÜ SAYILARLA İŞLEMLER

SONRAKİ BÖLÜM

BÖLÜM 2: ONDALIK GÖSTERİMİN ÇÖZÜMLEMESİ

 

SINIF 8KONULARKONU 16BÖLÜM 1

İLGİNİZİ ÇEKEBİLİR

8. SINIF KONU ANLATIMI
ÇARPAN NEDİR - ÇÖZÜMLÜ KONU TESTİ
DERS ÇALIŞMA PROGRAMI HAZIRLIYORUZ
SON 5 YILIN ÇIKMIŞ TEOG VE LGS SORULARI