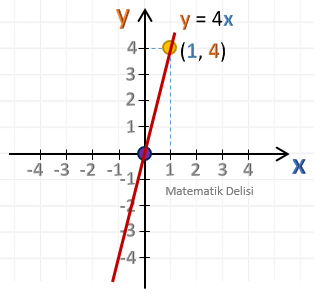
BÖLÜM 9: y = mx + n DENKLEMİNİN GRAFİĞİ
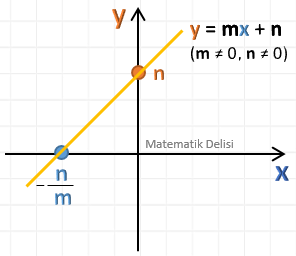
m ve n sıfırdan farklı gerçek sayılar olmak üzere,
- x-eksenini ... noktasından ve
- y-eksenini ... noktasından
kesen doğrudur.
![]()
... ...
⇒ ... ...
⇒ ... ...
Bu denklemde ... ve ...'dir.

n = 0 için
- orijinden (
0 ,0 ) ve - (
1 ,m ) noktasından
geçen bir doğrudur.
![]() Koordinat sisteminde, iki farklı noktadan yalnız bir doğru geçer.
Koordinat sisteminde, iki farklı noktadan yalnız bir doğru geçer.

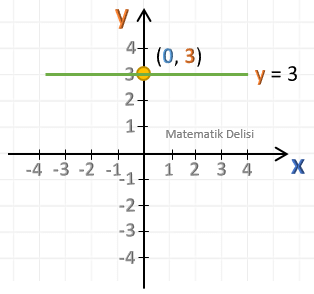
m = 0 için
- y-eksenini n noktasından kesen ve
- x-eksenine paralel (y-eksenine dik)
bir doğrudur.
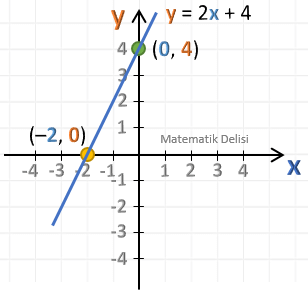
y = 2x + 4 denkleminin grafiğini çizelim.
y = 2x + 4 denkleminin grafiği, y-eksenini ... ve x-eksenini ... noktasından kesen bir doğrudur. Bu doğru, koordinat sisteminde aşağıdaki gibi gösterilir.
![]() Bir denkleme ait grafiğin x ve y-eksenlerini kestiği noktaları, bu denklemde sırasıyla
Bir denkleme ait grafiğin x ve y-eksenlerini kestiği noktaları, bu denklemde sırasıyla
y yerine 0 yazdığımızdax için bulduğumuz değer, grafiğin x-eksenini kestiği noktayı vex yerine 0 yazdığımızday için bulduğumuz değer, grafiğin y-eksenini kestiği noktayı verir.
... denkleminin grafiğini çizelim.
y = 0 içinx = 2'dir....
⇒ ...
⇒ ...
x = 0 içinsey = –1'dir....
⇒ ...
x-eksenini

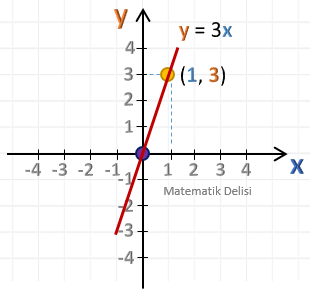
y = 3x denkleminin grafiğini çizelim.
y = 3 denkleminin grafiğini çizelim.
Aşağıda denklemlerin grafiklerini çizin.
a) y = –x + 2, b) y = 2x – 3, c) y = 4x, d) y = –3