BÖLÜM 3: KAREKÖKLÜ İFADEYİ TAM SAYI YAPAN ÇARPANLAR
... ile
...'yi çarptığımızda sonucun tam sayı olabilmesi için
...'nin
bir tam kare sayı olması gerekir.
İlk bölümde öğrendiğimiz gibi, ... ile ...'nin çarpımı ...'ye eşittir. Bu ifadenin bir tam sayıya eşit olabilmesi için karekök içerisindeki ...'nin bir tam kare sayı olması gerekir.
... sayısını ... ile çarpalım.
... ile aşağıdakilerden hangisinin çarpımının bir tam sayıya eşit olduğunu bulalım.
A) ... B) ... C) ... D) ...
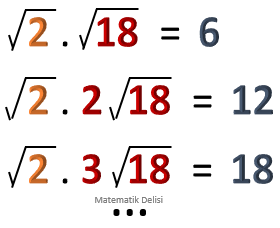
Kareköklü bir sayı ile çarpıldığında sonucu tam sayı yapan bir çarpan bulduğumuzu düşünelim. Kareköklü sayıyı bu çarpanın
herhangi bir tam katı ile çarptığımızda da sonuç tam sayı çıkar. Buna göre, sonucu tam sayı yapan sonsuz tane çarpan bulabiliriz.
Kenar uzunluklarından biri ... cm olan bir dikdörtgenin alanı santimetrekare cinsinden bir tam sayıya eşitse, diğer kenar uzunluğu kaç santimetre olabilir?
Bu soruyu çözebilmek için ... ile çarpıldığında sonucu tam sayı yapan çarpanı bulmamız gerekir.
...'ü kendisi ile çarptığımızda sonuç 3 olduğu için diğer kenar uzunluğu da ... cm olabilir. Yalnız bu sorunun birden fazla çözümü vardır. ...'ün tam katlarından herhangi biri, alanın tam sayı olmasını sağlar.
...
...
...
...
....
Aşağıdaki sayılardan hangi ikisi çarpıldığında sonucun tam sayı olacağını bulun.
a) ... b) ... c) ... d) ... e) ... f) ... g) ... h) ...
