---

BÖLÜM 1: POZİTİF VE NEGATİF TAM SAYILARIN NEGATİF KUVVETLERİ

Önceki konularda pozitif ve negatif tam sayıların pozitif kuvvetlerini almayı öğrenmiştik. Bu konuda ise, hem pozitif hem de negatif sayıların negatif kuvvetlerinin nasıl alındığını öğreneceğiz.

ÜSLÜ GÖSTERİMİ KENDİ TABANI İLE ÇARPMA

Üslü gösterimdeki kuvvet, tabandaki sayıdan kaç tanesinin birbiri ile çarpıldığını gösterir. Bu nedenle bir üslü sayıyı kendi tabanı ile çarptığımızda, çarpılan taban sayısını (veya kuvveti) 1 arttırmış oluruz. Örneğin, 5²⁰ sayısı 20 tane 5'in çarpımına eşittir. Bu sayıyı 5 ile çarptığımızda, 21 tane 5'in çarpımını veya 5²¹ sayısını elde ederiz.

ÜSLÜ GÖSTERİMİ KENDİ TABANINA BÖLME

Benzer şekilde, bir üslü sayıyı kendi tabanına böldüğümüzde, kuvveti 1 azaltmış oluruz. . Örneğin, 5²⁰, 20 tane 5'in çarpımına eşittir. Bu sayıyı 5'e böldüğümüzde, sonuç 19 tane 5'in çarpımına veya 5¹⁹'a eşit olur.

NEGATİF KUVVETLER

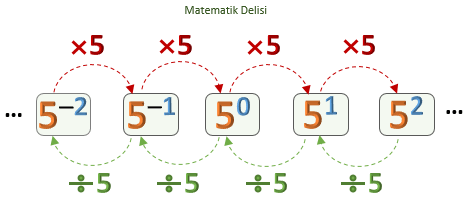
Bir üslü sayıyı kendi tabanına bölmeye devam edip, her adımda kuvvetten 1 çıkarırsak, belli bir süre sonra negatif kuvvetlerle karşılaşmaya başlarız. Örneğin,

• 5⁰'ı 5'e böldüğümüzde 5^–1 gösterimini;
• 5^–1'i 5'e böldüğümüzde ise 5^–2 gösterimini elde ederiz.

NEGATİF KUVVETLERİN KESİRLE GÖSTERİMİ

Genel olarak, ... ve ... gerçek sayılar olmak üzere, ... sıfırdan farklıysa aşağıdaki eşitliği yazabiliriz.

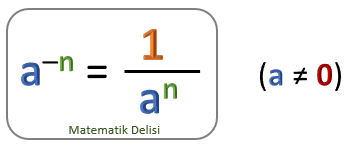
Negatif ve pozitif tüm ... sayıları için bu kural geçerlidir. Şimdi de, bu formülü 2 ve –2 sayılarının kuvvetlerini bulmak için kullanalım.

NEGATİF KUVVETLER
Kuvvet	2'nin kuvvetleri	–2'nin kuvvetleri
–1	... ...	... ...
–2	... ...	... ...
–3	... ...	... ...
–4	... ...	... ...
–5	... ...	... ...
–6	... ...	... ...
–7	... ...	... ...

Negatif sayıların çift kuvvetleri pozitif, tek kuvvetleri ise negatiftir. Örneğin, (–2)^–2'nin kuvveti çift olduğu için değeri pozitiftir; (–2)^–3'nin kuvveti tek olduğu için değeri negatiftir.

1’İN NEGATİF KUVVETLERİ

1'in tüm negatif kuvvetleri 1'e eşittir. Bunu, yukarıdaki formülde a yerine 1 koyarak görebiliriz.

... ...

–1’İN NEGATİF KUVVETLERİ

–1'in çift kuvvetleri 1'e eşittir.

... ... (n bir çift sayıysa)

–1'in tek kuvvetleri –1'e eşittir.

... ... (n bir tek sayıysa)

→KONU ANASAYFASINA DÖN←