BÖLÜM 2: BASİT OLAYLARIN OLASILIKLARI
Bu bölümde, eşolasılıklı bir deneyde bir olayın gerçekleşme ve gerçekleşmeme olasılıklarını nasıl bulabileceğimizi öğreniyoruz. Bu konuya ilişkin örnekleri sonraki bölümlerde inceliyoruz.
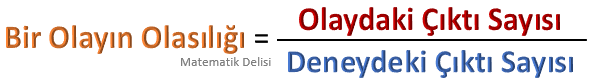
Bir olasılık deneyindeki çıktıların olasılıkları birbirine eşitse, bir olayın olasılığını bulabilmek için bu
olaya ait çıktıların sayısını, tüm çıktıların sayısına böleriz.
... çıktısı olan eşolasılıklı bir deneyde, her bir çıktının olasılığı ...'ye eşittir.
Olay, çıktılar kümesinin alt kümesidir. Bir olayın olasılığını bulabilmek için bu olaydaki çıktıların olasılıklarını toplarız.
Buna göre, bir olayda ... tane çıktı varsa, bu olayın olasılığı ... tane ...'nin toplamına veya ...'ye eşit olur.
BİR OLAYIN GERÇEKLEŞMEME OLASILIĞI
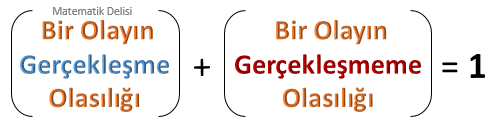
Bir olayın gerçekleşme ve gerçekleşmeme olasılıklarının toplamı 1'e eşittir.
- Atılan bir zarın çift olma ve çift olmama olasılıklarının toplamı 1'dir.
- Yarın bu saatte havanın yağışlı olma ve yağışlı olmama olasılıklarının toplamı 1'dir.
- Lise giriş sınavında 1. olma olasılığınız ile 1. olmama olasılığınızın toplamı 1'dir.
Bir olayın olma ve olmama olasılıklarının toplamının neden 1'e eşit olduğunu anlamak için çıktılar kümesini kullanabiliriz. Bir olaya ait alt kümeyi belirlediğimizde, çıktılar kümesini ikiye bölmüş oluruz. Bu kümelerden
- birinde sadece olaya ait çıktılar,
- diğerinde ise olaya ait olmayan çıktılar
bulunur.
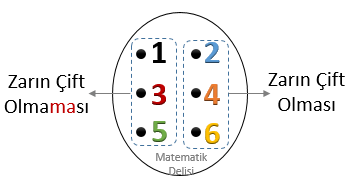
- İlk küme, olayın gerçekleşme durumunu,
- İkinci küme ise olaya ait olmayan tüm çıktıları veya başka bir deyişle bu olayın gerçekleşme
me si durumunu
ifade eder. Çıktılar kümesinin tamamını kapsadığı için bu kümelerin olasılıklarının toplamı 1'dir.
Bir olayın gerçekleşme olasılığını 1'den çıkardığımızda, bu olayın gerçekleşme
Sonraki üç bölümde, sırasıyla,
ile ilgili örnekler üzerine yoğunlaşıyoruz.
