ÇIKMIŞ SORULAR: GEOMETRİK CİSİMLERLE İLGİLİ ÇIKMIŞ LGS SORULARI VE ÇÖZÜMLERİ-2
| LGS'DE ÇIKAN SORU SAYISI | |||||||
|---|---|---|---|---|---|---|---|
| 2017-2018 | 2018-2019 | 2019-2020 | 2020-2021 | 2021-2022 | 2022-2023 | 2023-2024 | |
| Soru Sayısı | 3 | 2 | 0 | 0 | 1 | 0 | 1 |
| LGS'DE ÇIKAN SORU SAYISI | |
|---|---|
| Soru Sayısı | |
| 2017-2018 | 3 |
| 2018-2019 | 2 |
| 2019-2020 | 0 |
| 2020-2021 | 0 |
| 2021-2022 | 1 |
| 2022-2023 | 0 |
| 2023-2024 | 1 |
Aşağıda, LGS'de geometrik cisimlerle ilgili çıkan soruları ve bu soruların çözümlerini bulabilirsiniz. Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanan bu sorular, her sayfada en fazla 3 soru olacak şekilde kronolojik sıralamaya göre yazılmıştır. Diğer soruları görebilmek için sonraki sayfaya geçebilirsiniz.
2018-2019 LGS
Aşağıda dikdörtgen şeklindeki A, B, C kartonlarının her birinden dörder adet verilmiştir.
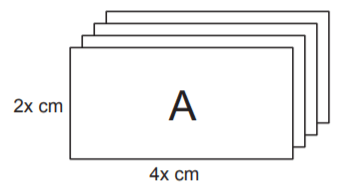


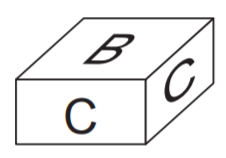
Bu kartonların kenarları çakıştırılarak iki tane kare prizma oluşturuluyor. Bu prizmalardan biri aşağıda verilmiştir.
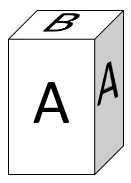
Kartonların tamamı kullanıldığına göre diğer prizmanın yüzey alanı kaç santimetrekaredir?
Çözüm:
İlk kare prizma için 2 tane B ve 4 tane C kartonu kullanılıyor. Buna göre ikinci kare prizma için geriye 2 tane B ve 4 tane A kartonu kalıyor.
A kartonunun yüzey alanı 2x . 4x = 8x2 cm2 ve B kartonunun yüzey alanı 2x . 2x = 4x2 cm2'dir. Buna göre, ikinci kare prizma için kullanılan kartonların toplam alanı
4 . 8x2 + 2 . 4x2 = 40x2 cm2'dir.
Bu alan, aynı zamanda, ikinci kare prizmanın yüzey alanına eşittir.
CEVAP: D
Dik üçgenlerde 90° lik açının karşısındaki kenara hipotenüs denir.
Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir.

a2 + c2 = b2
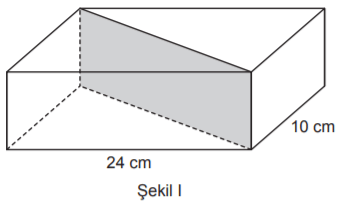
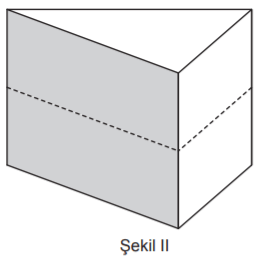
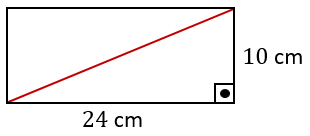
Taban ayrıtlarının uzunlukları 10 cm ve 24 cm olan dikdörtgenler prizması biçimindeki tahta blok Şekil I’deki gibi taban köşegenleri boyunca tabanlara dik olacak şekilde kesilerek iki eş parçaya ayrılıyor. Elde edilen iki parça üst üste yapıştırılarak Şekil II’deki dik üçgen dik prizma biçiminde bir tahta blok oluşturuluyor.
Elde edilen dik üçgen dik prizma ile başlangıçta verilen dikdörtgenler prizmasının ayrıtlarının uzunlukları toplamı birbirine eşittir.
Buna göre dikdörtgenler prizması şeklindeki tahta bloğun yüksekliği kaç santimetredir?
Çözüm:
Dikdörtgenler Prizması:
Dikdörtgenler prizmasının yüksekliği x ile ifade edildiğinde, ayrıt uzunluklarının toplamı 4(24 + 10 + x) = 136 + 4x cm olur.
Dik Üçgen Dik Prizma:
Pisagor Teoremi kullanılarak, dikdörtgenler prizmasının taban köşegeninin 26 cm olduğu görülebilir.
... ... ... cm
Buna göre, dik üçgen dik prizmanın ayrıt uzunluklarının toplamı 2(26 + 10 + 24) + 3 . 2x = 120 + 6x cm'dir.
Denklem:
x cinsinden bulunan ifadeler eşitlendiğinde aşağıdaki denklem elde edilir.
136 + 4x = 120 + 6x
⇒ 136 – 120 = 6x – 4x
⇒ 16 = 2x
⇒ x = 8 cm
Buna göre, dikdörtgenler prizmasının yüksekliği 8 cm'dir.
CEVAP: A
2021-2022 LGS

Yarıçapının uzunluğu r, yüksekliği h olan dik dairesel silindirin hacmi πr2h dir.

Yukarıda bir ürüne ait dik dairesel silindir şeklindeki konserve kutusu ve bu kutunun açınımı verilmiştir. Bu açınım üzerinde, alanı 100 cm2 olan mavi karesel bölgenin kenarları, yanal yüzeyin kenarlarına paraleldir. Mavi bölgenin kenarlara uzaklıkları ise şekildeki gibi 3 cm ve 7 cm'dir.
Buna göre, bu konserve kutusunun hacmi kaç santimetreküptür?
(π yerine 3 alınız.)
Çözüm:
Alanı 100 cm2 olan bir karenin kenar uzunluğu ... cm'dir. Buna göre, yanal yüzün yüksekliği 3 + 10 + 3 = 16 cm ve genişliği 7 + 10 + 7 = 24 cm'dir.
Tabanın yarıçapına r dersek, çevresi 2πr olur. Tabanın çevre uzunluğu aynı zamanda açınımdaki dikdörtgenin genişliğine eşittir. Dolayısıyla,
2πr = 24
⇒ πr = 12
⇒ r = 4'tür. (π = 3 için)
Yarıçapı 4 olan dairenin alanı
πr2 = 3 . 16 = 48 cm2'dir. (π = 3 için)
Küpün hacmini bulabilmek için taban alanı ile yanal yüzün yüksekliğini çarparız.
H = 48 × 16 = 768 cm3
CEVAP: C
