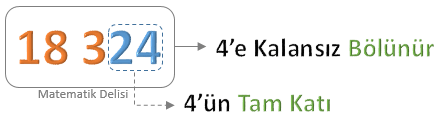
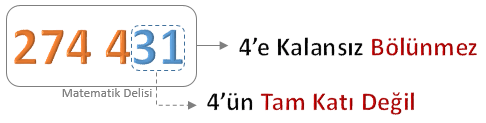
Bir doğal sayının 4’e kalansız bölünebilmesi için son iki basamağındaki sayının 4’ün tam katı veya 00 olması gerekir.

ÖRNEKLER:

75 612’nin son iki basamağındaki sayı 12’dir. 12, 4’ün tam katı olduğu için 75 612, 4’e kalansız bölünür.
8000’in son iki basamağındaki sayı 0’dır. Bu nedenle 8000 sayısı 4’e kalansız bölünür.
7308’in son iki basamağındaki sayı 8’dir ve bu sayı 4’ün katıdır. Bu nedenle 7308, 4’e kalansız bölünür.
83 715’in son iki basamağındaki sayı 15’tir. Bu sayı 4’ün tam katı olmadığı için 83 715, 4’e kalansız bölünmez.

ÖRNEKLER:

Aşağıdaki sayılar 4’e kalansız BÖLÜNÜR.

• 9392

• 8204

• 75 316

• 86 232

• 8360

• 7584

• 128

• 963 200

• 123 000 176

ÖRNEKLER:

Aşağıdaki sayılar 4’e kalansız BÖLÜNMEZ.

• 63 402

• 8610

• 7686

• 55 313

• 59 317

• 44 444 442

• 366

• 58 324 501

• 6 538 977

Alıştırmalar-3

Aşağıdaki sayılardan hangilerinin 4’e kalansız bölündüğünü bulun.

a) 7632, b) 666, c) 900, d) 231, e) 45 621, f) 808, g) 1212, h) 4355, i) 7801, j) 5673, k) 42 316

4’e kalansız bölünebilen sayıların tamamı çifttir ve 2’ye kalansız bölünür.

4’e bölünebilme, sadece son iki basamaktaki rakamla ilgilidir.

Aşağıdaki aracı kullanarak istediğiniz sayının 4'e kalansız bölünüp bölünmediğini ve 4'e bölümünden kalanı öğrenebilirsiniz.

BÖLÜNEBİLME KURALLARI-ÖZET
Sayı	Bölünebilme kuralı
2	Birler basamağındaki rakam çift olmalı.
3	Rakamların toplamı 3'ün tam katı olmalı.
4	Son iki basamağındaki sayı 4'ün tam katı veya 00 olmalı.
5	Birler basamağındaki rakam 0 veya 5 olmalı.
6	2 ve 3'e kalansız bölünebilmeli.
9	Rakamların toplamı 9'un tam katı olmalı.
10	Birler basamağındaki rakam 0 olmalı.