---

BÖLÜM 1: RASYONEL SAYILAR

Rasyonel sayılar kümesi ... ile gösterilir.

Tanımdaki "yazılabilen" kelimesine dikkat etmemiz gerekir. Bir sayı ... biçiminde yazılmamış olsa dahi, rasyonel olabilir. Önemli olan, bu şekilde yazılabiliyor olmasıdır. Örneğin, 3 sayısı ... formunda değildir. Yalnız, ... şeklinde de yazılabileceği için 3 sayısı rasyoneldir.

0'a bölme işlemi tanımsız olduğundan, tanımdaki ...'nin 0'dan farklı bir tam sayı olduğunu varsayabiliriz.

HANGİ SAYILAR RASYONELDİR?

A) BASİT, BİLEŞİK VE TAM SAYILI KESİRLER

Payı ve paydası tam sayı olan tüm basit, bileşik ve tam sayılı kesirler rasyoneldir. Çünkü basit ve bileşik kesirler ... şeklinde gösterilir ve tam sayılı kesirleri bu şekle dönüştürülebilir.

B) TAM SAYILAR VE DOĞAL SAYILAR

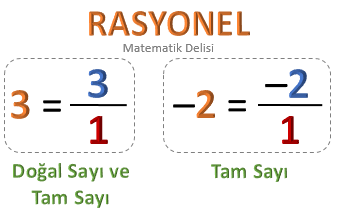
Tam sayıların tümü rasyoneldir. Çünkü herhangi bir ... tam sayısı, ... şeklinde yazılabilir.

Doğal sayıların tümü aynı zamanda tam sayı olduğu için doğal sayılar da rasyoneldir.

Doğal sayılar kümesi, tam sayılar kümesinin; tam sayılar kümesi ise rasyonel sayılar kümesinin alt kümesidir. Bu kümeler arasındaki ilişki aşağıda gösterilmiştir.

C) ONDALIK GÖSTERİM

Ondalık kısmında sonlu sayıda rakam bulunan ondalık gösterimler rasyoneldir çünkü bu sayılar payında ve paydasında tam sayı olan kesirlere kolayca dönüştürülebilir. Örneğin, ... sayısı ... biçiminde de yazılabilir.

D) DEVİRLİ SAYILAR

Aşağıdaki formül kullanılarak ... şekline dönüştürülebildiği için devirli sayılar rasyoneldir.

Bu formülde, ondalık kısımla aynı basamak sayısına sahip bir sayı oluşturuyoruz. Bu sayının

• En yüksek basamaklarına, devirli kısımdaki basamak sayısı kadar 9 ve
• En düşük basamaklarına, virgülden sonraki devirsiz basamak sayısı kadar 0

koyuyoruz. Oluşturduğumuz sayıya (z) diyelim. Buna ek olarak

• Virgül atıldıktan sonra ortaya çıkan tam sayıya (x) ve
• Virgül ve devirli basamaklar atıldıktan sonra ortaya çıkan tam sayıya (y) diyelim.

Devirli sayıya eşit olan bir kesir oluşturmak için paya (x) ile (y)'nin farkını ve paydaya (z) sayısını yazarız.

E) BAZI SAYILARIN KAREKÖKLERİ

Tam kare sayıların karekökleri rasyoneldir. Örneğin, ... ve ... sayıları rasyoneldir.

Bir ondalık gösterimin, ondalık kısmında çift sayıda basamak varsa ve virgül atıldığında ortaya bir tam sayı çıkıyorsa, bu gösterimin karekökü bir rasyonel sayıdır. (Ondalık gösterimin karekökünü nasıl hesapladığımızı hatırlamıyorsanız tıklayın.)

F) RASYONEL SAYILAR ARASINDA YAPILAN DÖRT İŞLEM SONUÇLARI

0'a bölmek gibi tanımsız bir işlem yapmadığımız sürece, rasyonel sayılar arasında sonlu sayıda dört işlem yaparak elde edebileceğimiz tüm sonuçlar rasyoneldir. Sonsuz tane işlemle irrasyonel bir sayı elde edebileceğimizi, üniversite seviyesinde öğreneceğiz.

→KONU ANASAYFASINA DÖN←