Sınıf 8 ➤ ÇIKMIŞ SORULAR ➤ LGS 2019 SORU VE ÇÖZÜMLERİ ➤ SORU 18
LİSELERE GİRİŞ SINAVI
LGS 2019 - Çıkmış Sorular ve Ayrıntılı Çözümleri SORU18
Aşağıdaki sorular Milli Eğitim Bakanlığı Yenilik ve Eğitim Teknolojileri Genel Müdürlüğü internet sitesinden alıntılanmıştır.
Dik üçgenlerde 90° lik açının karşısındaki kenara hipotenüs denir.
Bir dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir.

a2 + c2 = b2
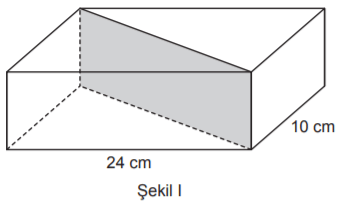
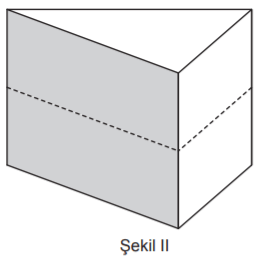
Taban ayrıtlarının uzunlukları 10 cm ve 24 cm olan dikdörtgenler prizması biçimindeki tahta blok Şekil I’deki gibi taban köşegenleri boyunca tabanlara dik olacak şekilde kesilerek iki eş parçaya ayrılıyor. Elde edilen iki parça üst üste yapıştırılarak Şekil II’deki dik üçgen dik prizma biçiminde bir tahta blok oluşturuluyor.
Elde edilen dik üçgen dik prizma ile başlangıçta verilen dikdörtgenler prizmasının ayrıtlarının uzunlukları toplamı birbirine eşittir.
Buna göre dikdörtgenler prizması şeklindeki tahta bloğun yüksekliği kaç santimetredir?
Çözüm:
Dikdörtgenler Prizması:
Dikdörtgenler prizmasının yüksekliği x ile ifade edildiğinde, ayrıt uzunluklarının toplamı 4(24 + 10 + x) = 136 + 4x cm olur.
Dik Üçgen Dik Prizma:
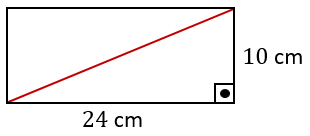
Pisagor Teoremi kullanılarak, dikdörtgenler prizmasının taban köşegeninin 26 cm olduğu görülebilir.
... ... ... cm
Buna göre, dik üçgen dik prizmanın ayrıt uzunluklarının toplamı 2(26 + 10 + 24) + 3 . 2x = 120 + 6x cm'dir.
Denklem:
x cinsinden bulunan ifadeler eşitlendiğinde aşağıdaki denklem elde edilir.
136 + 4x = 120 + 6x
⇒ 136 – 120 = 6x – 4x
⇒ 16 = 2x
⇒ x = 8 cm
Buna göre, dikdörtgenler prizmasının yüksekliği 8 cm'dir.
CEVAP: A
Sınıf 8 ➤ ÇIKMIŞ SORULAR ➤ LGS 2019 SORU VE ÇÖZÜMLERİ ➤ SORU 18
