Soru 11:

Dikdörtgen şeklindeki bir kâğıt, alanları santimetrekare cinsinden 10’dan büyük birer tam kare pozitif tam sayıya eşit olan karesel bölgelere aşağıdaki gibi ayrılmıştır.

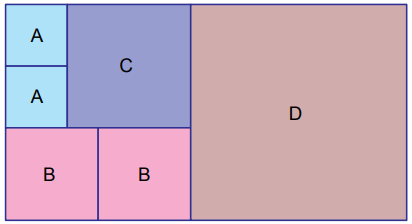
Eşit alanlı bölgeler aynı harf ile gösterildiğine göre dikdörtgen şeklindeki bu kâğıdın bir yüzünün alanı en az kaç santimetrekaredir?

A) 168

B) 255

C) 364

D) 392

Çözüm:

10'dan büyük tam kare sayıların en küçüğü 16 olduğu için en küçük kare olan A'nın alanı en az 16 cm²'dir. Bu durumda, A'nın kenar uzunluğu ... cm ve C'nin kenar uzunluğu 4 + 4 = 8 cm olur.

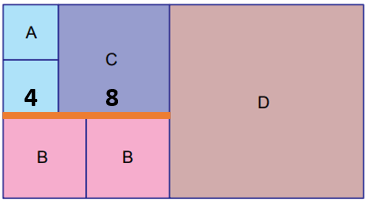
A ve C'nin kenar uzunluklarının toplamı B'nin kenar uzunluğunun 2 katına eşittir. Dolayısıyla, B'nin kenar uzunluğu (4 + 8) ÷ 2 = 6 cm'dir.

D'nin kenar uzunluğu 8 + 6 = 14 cm'dir.

Yukarıda bulduğumuz kenar uzunluklarına göre toplam alan 364 cm²'dir.

4² + 4² + 8² + 6² + 6² + 14² = 364 cm²

CEVAP: C