Soru 13:

Kısa kenarlarının uzunlukları x cm olan dikdörtgen şeklindeki 12 adet kâğıt uzun kenarlarından çakıştırılarak aşağıdaki şekil elde edilmiştir.

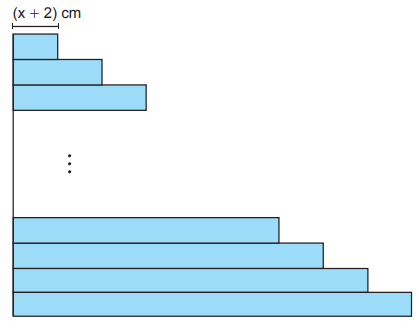
Bu kağıtlar; en üstteki kâğıdın uzun kenarının uzunluğu (x + 2) cm olmak üzere sonraki her kâğıt, bir önceki kâğıttan 2 cm daha uzun olacak biçimde yerleştirilmiştir.

Buna göre, oluşan şeklin bir yüzünün alanını santimetrekare cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?

A) 24x² + 312x

B) 24x² + 156

C) 12x² + 312

D) 12x² + 156x

Çözüm:

Mavi kâğıtların uzun kenarları, yukarıdan aşağı doğru sırasıyla, x + 2 cm, x + 4 cm, x + 6 cm, ... ve x + 24 cm'dir. Her birinin kısa kenarı x cm'dir. Kenar uzunluklarını çarparak bu kâğıtların alanlarını sırasıyla aşağıdaki gibi elde edebiliriz.

x(x + 2) = x² + 2x cm²

x(x + 4) = x² + 4x cm²

x(x + 6) = x² + 6x cm²

...

x(x + 24) = x² + 24x cm²

Bu alanların toplamı sorudaki şeklin bir yüzünün alanına eşittir. 12 tane x²'nin toplamı 12x² ve x'li terimlerin katsayılarının toplamı 156'dır. (2 + 4 + 6 + ... + 24 = 156) Buna göre toplam alan 12x² + 156x cm²'dir.

CEVAP: D