Soru 11:

Dikdörtgen şeklindeki bir kâğıt aşağıdaki gibi altı dikdörtgensel bölgeye ayrılmış ve bu bölgelerden bazılarının alanları şekil üzerinde gösterilmiştir.

Elde edilen bu dikdörtgensel bölgelerden her birinin kenarlarının uzunlukları santimetre cinsinden 1'den büyük birer doğal sayıdır.

Buna göre bu kâğıdın bir yüzünün alanı, santimetrekare cinsinden aşağıdakilerden hangisi olabilir?

A) 154

B) 162

C) 180

D) 196

Çözüm:

Soruda verilen birimler temel alındığında dikdörtgensel bölgelerin kenar uzunlukları, alanlarının 1'den büyük çarpanları olur.

• 35'in çarpanları : 1, 5, 7, 35
• 21'in çarpanları : 1, 3, 7, 21
• 44'ün çarpanları : 1, 2, 4, 11, 22, 44
• 33'ün çarpanları : 1, 3, 11, 33

35 ve 21 sayılarının 1'den büyük tek ortak çarpanı 7'dir. Buna göre, alanı 35 cm² ve 21 cm² olan bölgelerin ortak kenar uzunluğu 7 cm'dir. Bu bölgelere ait diğer kenar uzunlukları ise 35 ÷ 7 = 5 cm ve 21 ÷ 7 = 3 cm'dir.

Benzer şekilde, 44 ve 33'ün 1'den büyük tek ortak çarpanı 11'dir. Dolayısıyla, alanı 44 cm² ve 33 cm² olan bölgelerin ortak kenar uzunluğu 11 cm'dir.

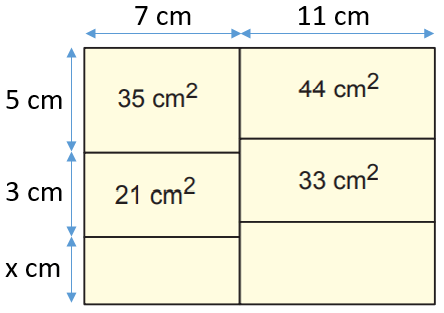
Bulduğumuz kenar uzunluklarını yerlerine yazdığımızda kâğıdın genişliğinin 7 + 11 = 18 cm olduğunu görebiliriz. Ayrıca, sol alttaki bölgenin yüksekliğine x dersek, kâğıdın yüksekliği toplam 8 + x çıkar. x, 1'den büyük bir tam sayı olduğu içi kâğıdın yüksekliği en az 8 + 2 = 10 cm'dir. Buna göre, bir yüzün alanı en az 18 . 10 = 180 cm²'dir.

CEVAP: C