Sınıf 8 ➤ ÖRNEK SORULAR ➤ ŞUBAT 2020

LİSELERE GİRİŞ SINAVI-ÖRNEK SORULAR

ŞUBAT 2020-LGS MATEMATİK-ÖRNEK SORULARININ ÇÖZÜMLERİ

Bu sayfada, MEB’in yayınladığı 2019-2020 LGS Şubat ayı örnek sorularının çözümlerini bulabilirsiniz. Soruları görmek için bu bağlantıyı tıklayabilirsiniz.

DİĞER AYLARIN ÖRNEK SORULARI VE ÇÖZÜMLERİ İÇİN TIKLAYIN!

ÖRNEK SORU 1’in Çözümü

Her halkadan 9’ar tane getirdiğinden, Gökçe öğretmenin bir cebirsel ifadeyi halkalarla gösterebilmesi için bu ifadedeki tüm katsayıların 9 veya 9’dan küçük olması gerekir. Seçeneklerdeki parantezleri açarak hangi seçenekteki cebirsel ifadenin bu şartı sağladığını bulabiliriz.

A) (x + 4)² = x² + 8x + 16

B) (2x + 3)² = 4x² + 12x + 9

C) (3x + 1)² = 9x² + 6x + 1

D) (3x + 2)² = 9x² + 12x + 4

A, B ve D seçeneklerindeki ifadelerde katsayıların birer tanesinin 9’dan büyük olduğunu görüyoruz. Tüm katsayıları 9 veya 9’dan küçük olan tek ifade C seçeneğinde verilmiştir.

CEVAP: C

İLGİLİ BAĞLANTILAR

ÖRNEK SORU 2’nin Çözümü

Otoparkın her bölümünde park yerlerinin 1’den 16’ya kadar numaralandırıldığını görüyoruz. Bu numaralardan asal olanlar 2, 3, 5, 7, 11 ve 13’tür.

Otoparkta toplam 4 bölüm ve her bölümde 6 asal sayı olduğu için Burhan’ın arabasını park etmiş olabileceği toplam 6 × 4 = 24 farklı olası park yeri vardır.

CEVAP: C

İLGİLİ BAĞLANTILAR

ÖRNEK SORU 3’ün Çözümü

1’den 48’e kadar olan tam kare sayılar 1, 4, 9, 16, 25 ve 36’dır. Bu sayılardan her biri yapının farklı bir katındadır. Buna göre,

16 katın 6’sında, üzerinde tam kare sayı yazan bloklar
Geriye kalan 10 katta, üzerinde tam kare olmayan sayı yazan bloklar çekilmiştir.

Çekilen 16 bloktan 6’sı tam kare olduğu için istenilen olasılık ...'dir.

CEVAP: C

İLGİLİ BAĞLANTILAR

ÖRNEK SORU 4’ün Çözümü

Bir daire grafiğindeki merkez açılar, parçaların bütüne olan oranlarını gösterir. C türünü ifade eden dilimin merkez açısı her iki daire grafiğinde de 360° – 90° – 120° = 150°’dir. Şubat ayındaki toplam köpek sayısı, ocak ayındakinin 2 katı olduğu halde, C türünün bütüne oranı aynı kalmıştır. Buna göre, C türünün şubat ayındaki sayısı, ocak ayındakinin 2 katı olmalıdır.

Seçeneklere baktığımızda sadece A ve C’deki sütun grafiklerinde C türündeki köpek sayısının 2 katına çıktığını görüyoruz. Fakat A seçeneğindeki grafiğe göre, yalnız C türünün değil, tüm türlerin sayısının 2 katına çıkması gerekirdi. Bu doğru olsaydı, daire grafiklerindeki tüm merkez açıların aynı kalması gerekirdi. A ve B türlerini gösteren daire dilimlerinin merkez açıları aynı kaldığı için A seçeneğini de eleyebiliriz. Böylece geriye sadece C seçeneği kalıyor.

CEVAP: C

İLGİLİ BAĞLANTILAR

ÖRNEK SORU 5’in Çözümü

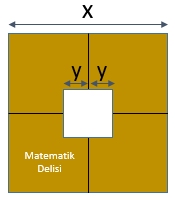
Kare biçimindeki parça kesilip atıldıktan sonra, kâğıt tekrar açıldığında yukarıdaki şekil elde edilir. Bu şekildeki büyük karenin alanı x . x = x² cm² ve kesilen küçük karenin alanı 2y . 2y = 4y² cm²’dir.

Buna göre, geriye kalan alan x² – 4y² cm² olmalıdır. Bu alana özdeş olan tek ifade D seçeneğinde verilmiştir.

x² – 4y² = (x – 2y)(x + 2y)

CEVAP: D

İLGİLİ BAĞLANTILAR

ÖRNEK SORU 6’nın Çözümü

İdil’in ders videosunu 1,0 x(normal) hız seçeneğinde ... dakika izleyebildiğini varsayalım. Buna göre, videonun ...’lük kısmını 1,0 x(normal) hız seçeneğinde izleseydi, izleme süresi ... dakika olurdu. 1,25 x(hızlı) hız seçeneği ile izlediği için bu kısmı bitirmesi

... ... ... dakika

sürmüştür.

Benzer şekilde, geriye kalan ...’lük kısmı 1,0 x(normal) hız seçeneğinde izleseydi, bu kısmın izlenme süresi ... dakika olurdu. 1,5 x(daha hızlı) hız seçeneğini kullandığı için bu süre

... ... ... dakika

sürmüştür.

A cinsinden toplam izlenme süresi

... ...

... dakikadır.

Bu ifadeyi 68’e eşitleyerek, A’nın kaç dakika olduğunu veren bir denklem oluşturabiliriz.

...

⇒ ...

⇒ ... dakika

CEVAP: C

İLGİLİ BAĞLANTILAR

ÖRNEK SORU 7’nin Çözümü

Sorudaki görseli, sağ profilden tekrar çizip, verilen uzunlukları bu görsel üzerinde gösterelim.

Karagözle perde arasında kalan uzaklığa ... cm dersek, sopanın sol ucu ile zemin arasındaki uzaklık ... cm olur. Buna göre, karagözü tutan sopanın sol ucu ile perde arasındaki uzaklığı hem ... ... cm ile hem de ... ... ... cm ile ifade edebiliriz.

Bulduğumuz iki cebirsel ifadeyi birbirine eşitleyerek, karagöz figürü ile perde arasındaki mesafeyi veren bir denklem oluşturabiliriz.

... ...

⇒ ... ...

⇒ ...

⇒ ... cm

CEVAP: C

İLGİLİ BAĞLANTILAR

ÖRNEK SORU 8’in Çözümü

Oteldeki tüm müşterilerin sayısına ... diyelim. Saat 17:00’daki yüzdelere tüm müşterilerin katılımıyla ulaşıldığı için “memnunum” seçeneğini işaretleyen müşteri sayısı ...’dur.

Saat 12:00 ile 17:00 arasında toplam 110 + 90 = 200 müşteri bu anketi doldurmuştur. Buna göre, saat 12:00’a kadar anketi dolduran toplam müşteri sayısı ...’dür. Şekildeki görsele göre, ... kişinin % 80’i “memnunum” seçeneğini tercih etmiştir. Bu sayı ...’e eşittir.

Saat 12:00 ile 17:00 arasında “memnumum” seçeneğini tercih eden kişi sayısı 110 olduğu için ...’dan ...’i çıkarıp 110’a eşitleyerek, toplam müşteri sayısını veren bir denklem oluşturabiliriz.

... ... ...

⇒ ... ... ...

⇒ ... ...

⇒ ...

CEVAP: B

İLGİLİ BAĞLANTILAR

ÖRNEK SORU 9’un Çözümü

Soruda verilen eş kağıtlardan birinin santimetre cinsinden genişliğine ... dersek,

ilk şekildeki katlanmış kağıdın genişliği ... cm’ye,
ikinci şekildeki katlanmış kağıdın genişliği ... cm’ye ve
üçüncü şekildeki katlanmış kağıdın genişliği ... cm’ye

eşit olur.

Poşet dosyada,

Üstte gösterilen toplam uzunluk santimetre cinsinden ... ile ve
Altta gösterilen toplam uzunluk santimetre cinsinden ... ... ile

ifade edilebilir. Bu iki uzunluğu birbirine eşitleyerek, eş kağıtlardan birinin genişliğini veren bir denklem oluşturabiliriz.

... ... ...

⇒ ... ... ...

⇒ ... ...

⇒ ...

⇒ ... cm

... cm sonucunu ... ifadesinde yerine yazarak, poşet dosyanın kısa kenar uzunluğunu bulabiliriz.

... ... ... cm

CEVAP: C

İLGİLİ BAĞLANTILAR

ÖRNEK SORU 10’un Çözümü

Uçangözün eczaneden dönüş süresine x dersek eczaneye gidiş-dönüş süresi 1,25x olur. Buna göre uçangözün gidiş-dönüşü toplam x + 1,25x = 2,25x dakika sürer.

Hafta boyunca, hava koşullarının uygun olduğu gün sayısı 3’tür. Buna göre uçangözün bir gidiş-dönüşü 108 ÷ 3 = 36 dakika sürmüştür.

2,25x’i 36 dakikaya eşitleyerek, x’in değerini bulabiliriz.

2,25x = 36

⇒ 4 . 2,25x = 4 . 36

⇒ 9x = 144

⇒ x = 16 dakika

Buna göre, uçangözün ecza deposundan eczaneye gidiş süresi 1,25 . 16 = 20 dakikadır.

CEVAP: B